Statistik adalah cabang matematika yang berfokus pada pengumpulan, analisis, interpretasi, dan penyajian data. Salah satu konsep penting dalam statistik adalah standar deviasi, yang digunakan untuk mengukur sejauh mana data tersebar dari nilai rata-ratanya. Dalam artikel ini, kita akan menjelajahi rumus standar deviasi dan bagaimana menggunakannya untuk menganalisis data.
Apa itu Standar Deviasi?
Standar deviasi adalah ukuran statistik yang digunakan untuk mengukur seberapa jauh data tersebar dari nilai rata-rata. Dalam konteks statistik, data dapat tersebar secara luas atau terkonsentrasi di sekitar nilai rata-rata. Standar deviasi memberikan gambaran tentang variasi data dan membantu kita memahami sejauh mana data kami terletak dari nilai rata-rata.
Standar deviasi dihitung dengan mengambil akar kuadrat dari varian data. Varian adalah ukuran statistik lain yang mengukur sejauh mana setiap titik data berbeda dari nilai rata-rata. Dengan menghitung varian dan mengambil akar kuadratnya, kita dapat mendapatkan standar deviasi.
Rumus Standar Deviasi
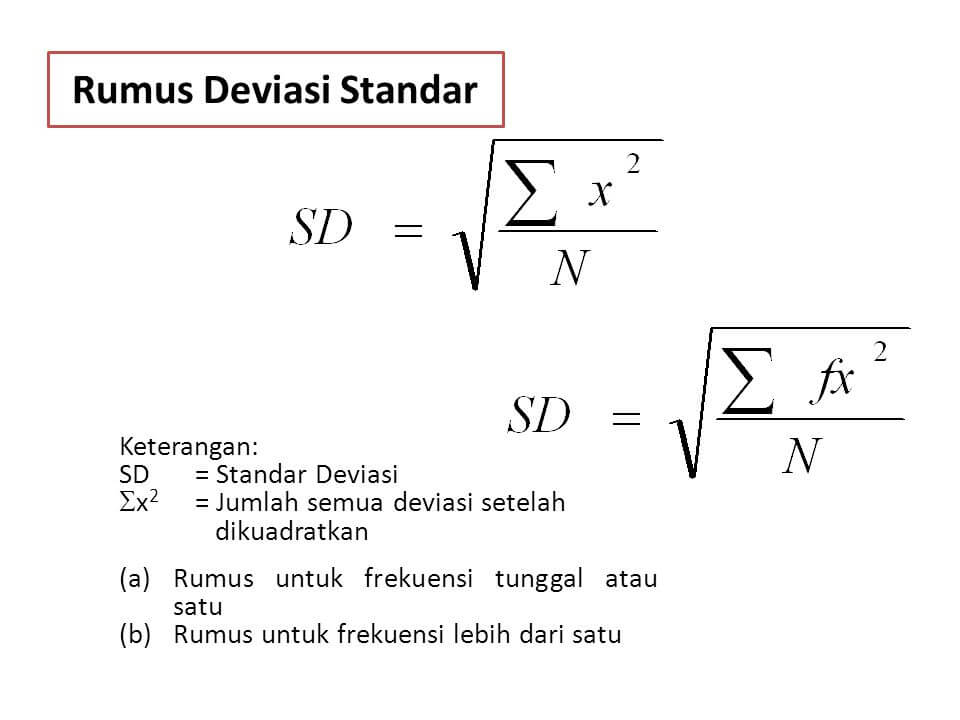
Rumus standar deviasi yang umum digunakan adalah sebagai berikut:
Standar Deviasi = √((Σ(x - μ)²) / N)
- Σ menunjukkan jumlah total.
- x adalah setiap titik data dalam sampel.
- μ adalah nilai rata-rata dari semua titik data.
- N adalah jumlah total titik data dalam sampel.
Dalam rumus ini, kita mengambil selisih kuadrat antara setiap titik data dan nilai rata-rata. Kemudian, kita menjumlahkan selisih kuadrat ini untuk semua titik data. Jumlah ini kemudian dibagi dengan jumlah total titik data dalam sampel, dan akar kuadrat hasilnya memberikan standar deviasi.
Contoh Penghitungan Standar Deviasi
Untuk memberikan pemahaman yang lebih baik tentang bagaimana rumus standar deviasi digunakan, mari kita lihat contoh penghitungannya. Misalkan kita memiliki data berikut: 12, 15, 18, 20, dan 22. Mari kita hitung standar deviasinya menggunakan rumus yang telah disebutkan sebelumnya.
Langkah pertama adalah menghitung nilai rata-rata dari data kita. Penjumlahan semua titik data dan membaginya dengan jumlah total titik data memberikan kita nilai rata-rata:
(12 + 15 + 18 + 20 + 22) / 5 = 87 / 5 = 17.4
Setelah mendapatkan nilai rata-rata, kita dapat menggunakan rumus standar deviasi untuk menghitung seberapa jauh data kita tersebar dari nilai rata-ratanya. Mari kita ikuti langkah-langkah rumus:
(12 - 17.4)² + (15 - 17.4)² + (18 - 17.4)² + (20 - 17.4)² + (22 - 17.4)² = 28.84 + 5.76 + 0.36 + 6.76 + 18.36 = 60.08
Setelah menghitung jumlah selisih kuadrat, kita membaginya dengan jumlah total titik data:
60.08 / 5 = 12.016
Terakhir, kita mengambil akar kuadrat dari hasil tersebut untuk mendapatkan standar deviasi:
√12.016 ≈ 3.47
Jadi, standar deviasi dari data kita adalah sekitar 3.47.
Penggunaan Standar Deviasi dalam Statistik
Standar deviasi adalah ukuran statistik yang penting dan sering digunakan dalam berbagai bidang. Berikut adalah beberapa contoh penggunaannya:
1. Analisis Keuangan
Dalam analisis keuangan, standar deviasi digunakan untuk mengukur risiko investasi atau portofolio. Semakin tinggi standar deviasi, semakin tinggi risiko potensialnya. Investor dan manajer keuangan menggunakan standar deviasi untuk memahami sejauh mana hasil investasi dapat bervariasi dari rata-rata yang diharapkan.
2. Ilmu Sosial
Dalam ilmu sosial, standar deviasi digunakan untuk menggambarkan variasi dalam data survei atau penelitian. Misalnya, dalam penelitian tentang pendapatan rumah tangga, standar deviasi dapat menunjukkan sejauh mana pendapatan individu bervariasi di dalam populasi yang diteliti.
3. Pengendalian Kualitas
Dalam pengendalian kualitas, standar deviasi digunakan untuk memonitor dan memastikan kualitas produk atau proses. Standar deviasi yang tinggi menunjukkan variasi yang besar dalam hasil produksi, yang dapat mengindikasikan masalah dalam proses produksi atau kekurangan konsistensi dalam kualitas hasil.
Faktor yang Memengaruhi Standar Deviasi
Beberapa faktor dapat memengaruhi besarnya standar deviasi dalam satu set data. Berikut adalah beberapa faktor yang perlu diperhatikan:
1. Variasi Data
Jumlah variasi dalam data akan mempengaruhi besarnya standar deviasi. Semakin bervariasinya data, semakin tinggi standar deviasinya. Sebaliknya, jika data cenderung terkonsentrasi di sekitar nilai rata-rata, standar deviasinya akan lebih rendah.
2. Ukuran Sampel
Ukuran sampel juga dapat mempengaruhi standar deviasi. Semakin besar sampel yang digunakan dalam perhitungan, semakin akurat standar deviasi tersebut. Dalam sampel yang lebih kecil, standar deviasi cenderung lebih tidak stabil dan mungkin tidak merepresentasikan variasi yang sebenarnya dalam populasi.
3. Outlier
Outlier, atau data yang secara signifikan berbeda dari nilai-nilai lain dalam set data, dapat mempengaruhi standar deviasi. Outlier dapat menyebabkan peningkatan atau penurunan yang signifikan dalam standar deviasi, tergantung pada sejauh mana outlier tersebut berbeda dari nilai-nilai lain.
Kesimpulan
Standar deviasi adalah ukuran statistik yang penting untuk mengukur sejauh mana data tersebar dari nilai rata-rata. Dalam artikel ini, kita telah menjelajahi rumus standar deviasi dan bagaimana menggunakannya untuk menganalisis data. Standar deviasi membantu kita memahami variasi dalam data dan dapat digunakan dalam berbagai bidang seperti analisis keuangan, ilmu sosial, dan pengendalian kualitas. Faktor yang memengaruhi standar deviasi termasuk variasi data, ukuran sampel, dan adanya outlier dalam data.
Pertanyaan yang Sering Diajukan (FAQs)
- Apa perbedaan antara standar deviasi dan simpangan baku?
- Bagaimana interpretasi standar deviasi?
- Apakah standar deviasi selalu positif?
- Apakah standar deviasi dapat menjadi nol?
- Kenapa standar deviasi penting dalam statistik?
Simpangan baku adalah ukuran statistik lain yang digunakan untuk mengukur penyebaran data. Perbedaan utamanya adalah simpangan baku dihitung dengan mengambil akar kuadrat dari varian sementara standar deviasi dihitung langsung dari varian.
Standar deviasi dapat diinterpretasikan sebagai ukuran variasi atau risiko dalam data. Semakin tinggi standar deviasi, semakin besar variasi atau risiko dalam data tersebut.
Ya, standar deviasi selalu positif karena dihitung dengan mengambil akar kuadrat dari varian, yang juga selalu positif.
Standar deviasi dapat menjadi nol jika semua titik data dalam sampel memiliki nilai yang sama. Ini menunjukkan bahwa tidak ada variasi dalam data.
Standar deviasi penting karena memberikan informasi tentang seberapa jauh data tersebar dari nilai rata-ratanya. Ini membantu kita memahami variasi dalam data dan dapat digunakan untuk mengambil keputusan yang lebih baik dalam berbagai bidang.
Ringkasan
Standar deviasi adalah ukuran statistik yang digunakan untuk mengukur seberapa jauh data tersebar dari nilai rata-ratanya. Rumus standar deviasi adalah √((Σ(x - μ)²) / N), di mana Σ adalah jumlah total, x adalah setiap titik data, μ adalah nilai rata-rata, dan N adalah jumlah total titik data. Standar deviasi digunakan dalam berbagai bidang seperti analisis keuangan, ilmu sosial, dan pengendalian kualitas. Beberapa faktor yang mempengaruhi standar deviasi adalah variasi data, ukuran sampel, dan adanya outlier dalam data. Dengan memahami dan menggunakan standar deviasi dengan benar, kita dapat mendapatkan wawasan yang berharga dari data statistik.