Standar deviasi adalah salah satu konsep kunci dalam statistika yang digunakan untuk mengukur sejauh mana data tersebar di sekitar nilai rata-ratanya. Dalam artikel ini, kita akan menjelaskan apa itu standar deviasi, bagaimana menghitungnya, dan mengapa ini penting dalam berbagai bidang, termasuk keuangan, ilmu sosial, dan ilmu alam. Kami juga akan melihat contoh penggunaan standar deviasi dalam kehidupan sehari-hari dan bagaimana kita dapat memanfaatkan informasi ini untuk membuat keputusan yang lebih baik.
Apa Itu Standar Deviasi?
Standar deviasi adalah ukuran statistik yang digunakan untuk mengukur sebaran data di sekitar nilai rata-rata. Ini memberikan gambaran tentang sejauh mana data tersebar dari nilai rata-rata dan seberapa variabel data tersebut. Standar deviasi digunakan untuk menganalisis data dalam berbagai bidang, termasuk ilmu pengetahuan, ekonomi, dan keuangan.
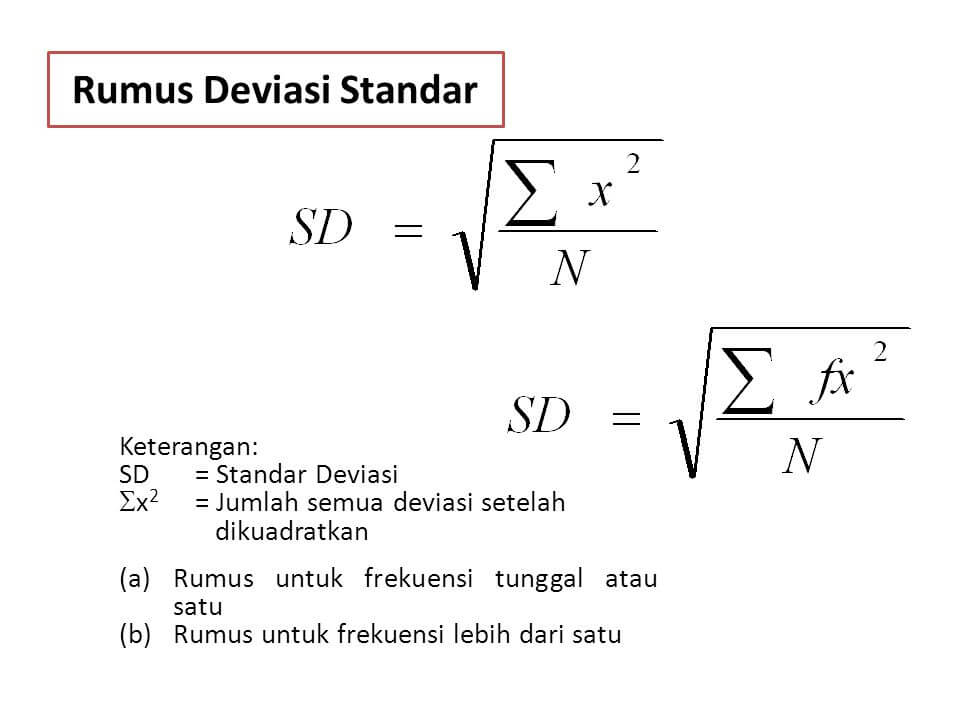
Standar deviasi dihitung dengan mengambil akar kuadrat dari varians. Varians adalah ukuran yang menghitung sejauh mana setiap titik data berbeda dari nilai rata-rata, kemudian menjumlahkan seluruh perbedaan tersebut dan membaginya dengan jumlah total data. Akar kuadrat dari varians memberikan standar deviasi.
Bagaimana Menghitung Standar Deviasi?
Untuk menghitung standar deviasi, ikuti langkah-langkah berikut:
- Hitung nilai rata-rata dari data yang diberikan.
- Hitung selisih antara setiap titik data dan nilai rata-rata.
- Kuadratkan hasil selisih dari langkah kedua.
- Jumlahkan semua hasil kuadrat dari langkah ketiga.
- Bagi jumlah hasil kuadrat dari langkah keempat dengan jumlah total data.
- Ambil akar kuadrat dari hasil pembagian pada langkah kelima.
Setelah mengikuti langkah-langkah ini, Anda akan mendapatkan standar deviasi dari data yang diberikan.
Penggunaan Standar Deviasi
Standar deviasi memiliki berbagai penggunaan dalam berbagai bidang. Berikut adalah beberapa contoh penggunaan standar deviasi:
1. Keuangan
Dalam dunia keuangan, standar deviasi digunakan untuk mengukur risiko investasi. Semakin tinggi standar deviasi, semakin besar fluktuasi nilai investasi dari waktu ke waktu. Investor sering menggunakan standar deviasi untuk memilih investasi yang sesuai dengan profil risiko mereka. Misalnya, investor dengan profil risiko rendah mungkin memilih investasi dengan standar deviasi yang lebih rendah, sementara investor dengan profil risiko tinggi mungkin lebih memilih investasi dengan standar deviasi yang lebih tinggi.
2. Ilmu Sosial
Dalam ilmu sosial, standar deviasi digunakan untuk menganalisis sebaran data dalam survei atau eksperimen. Misalnya, dalam survei kepuasan pelanggan, standar deviasi dapat memberikan informasi tentang sejauh mana tanggapan pelanggan bervariasi. Standar deviasi yang tinggi menunjukkan adanya variasi yang besar dalam tanggapan pelanggan, sementara standar deviasi yang rendah menunjukkan bahwa tanggapan pelanggan cenderung seragam.
3. Ilmu Alam
Dalam ilmu alam, standar deviasi digunakan untuk menganalisis data percobaan dan mengukur tingkat ketepatan hasil. Standar deviasi yang rendah menunjukkan bahwa data percobaan cenderung mendekati nilai rata-rata yang sebenarnya, sedangkan standar deviasi yang tinggi menunjukkan adanya variasi yang besar di antara hasil percobaan. Standar deviasi juga digunakan dalam analisis regresi untuk mengukur seberapa baik model statistik cocok dengan data yang diamati.
Keuntungan Menggunakan Standar Deviasi
Penggunaan standar deviasi memiliki beberapa keuntungan yang signifikan:
1. Mengukur Risiko
Standar deviasi membantu mengukur risiko dalam berbagai konteks, termasuk keuangan dan investasi. Dengan memahami sejauh mana data tersebar dari nilai rata-rata, investor dapat membuat keputusan yang lebih bijaksana tentang alokasi aset mereka dan mengelola risiko dengan lebih efektif.
2. Menentukan Tingkat Ketepatan
Dalam ilmu alam, standar deviasi digunakan untuk menentukan tingkat ketepatan hasil percobaan. Semakin rendah standar deviasi, semakin tinggi tingkat ketepatan hasil percobaan. Informasi ini penting dalam memahami validitas hasil percobaan dan menentukan apakah perlu dilakukan penyesuaian atau perbaikan dalam metode pengukuran atau pengujian.
3. Memahami Variabilitas Data
Dengan memahami standar deviasi, kita dapat mendapatkan pemahaman yang lebih baik tentang variasi dalam data. Ini membantu dalam pengambilan keputusan yang lebih baik dan analisis yang lebih akurat. Misalnya, jika kita memahami bahwa sebaran data dalam suatu populasi sangat luas, kita dapat mengambil langkah-langkah untuk mengurangi variabilitas dan meningkatkan kualitas produk atau layanan.
Contoh Penggunaan Standar Deviasi dalam Kehidupan Sehari-hari
Standar deviasi dapat ditemukan dalam banyak aspek kehidupan sehari-hari kita. Berikut adalah beberapa contoh penggunaannya:
1. Pengukuran Kinerja
Dalam dunia bisnis, standar deviasi digunakan untuk mengukur kinerja karyawan. Dengan membandingkan kinerja individu dengan standar deviasi dari seluruh kelompok, manajer dapat mengidentifikasi karyawan yang berkinerja tinggi atau rendah dibandingkan dengan rekan-rekan mereka. Informasi ini dapat digunakan untuk memberikan penghargaan atau memberikan pelatihan tambahan kepada karyawan yang membutuhkannya.
2. Olahraga
Standar deviasi digunakan dalam olahraga untuk menganalisis kinerja atlet. Misalnya, dalam olahraga seperti tenis atau golf, standar deviasi dapat digunakan untuk mengukur konsistensi atlet dalam permainan mereka. Atlet dengan standar deviasi yang rendah menunjukkan konsistensi yang lebih besar dalam performa mereka, sementara atlet dengan standar deviasi yang tinggi mungkin mengalami fluktuasi yang lebih besar dalam performa mereka dari waktu ke waktu.
3. Penelitian Medis
Standar deviasi digunakan dalam penelitian medis untuk menganalisis data klinis. Misalnya, dalam uji klinis untuk menguji efektivitas obat, standar deviasi dapat memberikan informasi tentang sejauh mana hasil pengobatan bervariasi di antara kelompok pasien. Informasi ini penting dalam menentukan apakah obat tersebut efektif secara konsisten atau hanya pada sebagian kecil pasien.
Frequently Asked Questions (FAQs)
1. Apa perbedaan antara standar deviasi dan varians?
Standar deviasi dan varians keduanya digunakan untuk mengukur sebaran data, tetapi standar deviasi memberikan gambaran yang lebih intuitif tentang variabilitas karena dalam satuan yang sama dengan data aslinya. Varians adalah kuadrat dari standar deviasi dan dinyatakan dalam satuan yang berbeda.
2. Bagaimana standar deviasi dipengaruhi oleh data ekstrem?
Standar deviasi dapat dipengaruhi oleh data ekstrem yang berada di luar jangkauan nilai rata-rata. Data ekstrem dapat menyebabkan standar deviasi menjadi lebih tinggi karena jarak antara nilai rata-rata dan data ekstrem lebih besar.
3. Apakah standar deviasi selalu lebih besar dari nol?
Tidak, standar deviasi tidak selalu lebih besar dari nol. Jika semua data memiliki nilai yang sama, standar deviasi akan menjadi nol karena selisih antara setiap titik data dan nilai rata-rata adalah nol.
4. Apakah standar deviasi bisa digunakan untuk data kategorikal atau nominal?
Standar deviasi biasanya digunakan untuk data interval atau rasio, yang memiliki urutan dan jarak antara nilai-nilai yang dapat diukur. Untuk data kategorikal atau nominal, ukuran sebaran yang lebih cocok adalah proporsi atau persentase.
5. Bagaimana cara menafsirkan standar deviasi?
Tingkat standar deviasi mengindikasikan seberapa jauh data tersebar di sekitar nilai rata-ratanya. Semakin tinggi standar deviasi, semakin besar variabilitas dalam data. Sebaliknya, semakin rendah standar deviasi, semakin sedikit variasi dalam data.
Kesimpulan
Standar deviasi adalah ukuran statistik yang penting dalam menganalisis sebaran data. Ini membantu kita memahami sejauh mana data tersebar dari nilai rata-rata dan seberapa variabel data tersebut. Standar deviasi digunakan di berbagai bidang, termasuk keuangan, ilmu sosial, dan ilmu alam, untuk mengukur risiko, menentukan tingkat ketepatan, dan memahami variasi dalam data.
Dalam kehidupan sehari-hari, standar deviasi dapat ditemukan dalam berbagai konteks, seperti pengukuran kinerja, olahraga, dan penelitian medis. Dengan memahami standar deviasi dan bagaimana menggunakannya, kita dapat membuat keputusan yang lebih baik dan mengambil langkah-langkah yang tepat dalam mengelola risiko atau meningkatkan kualitas produk atau layanan.
Pertanyaan yang Sering Diajukan (FAQs)
1. Apa perbedaan antara standar deviasi dan varians?
Standar deviasi dan varians keduanya digunakan untuk mengukur sebaran data, tetapi standar deviasi memberikan gambaran yang lebih intuitif tentang variabilitas karena dalam satuan yang sama dengan data aslinya. Varians adalah kuadrat dari standar deviasi dan dinyatakan dalam satuan yang berbeda.
2. Bagaimana standar deviasi dipengaruhi oleh data ekstrem?
Standar deviasi dapat dipengaruhi oleh data ekstrem yang berada di luar jangkauan nilai rata-rata. Data ekstrem dapat menyebabkan standar deviasi menjadi lebih tinggi karena jarak antara nilai rata-rata dan data ekstrem lebih besar.
3. Apakah standar deviasi selalu lebih besar dari nol?
Tidak, standar deviasi tidak selalu lebih besar dari nol. Jika semua data memiliki nilai yang sama, standar deviasi akan menjadi nol karena selisih antara setiap titik data dan nilai rata-rata adalah nol.
4. Apakah standar deviasi bisa digunakan untuk data kategorikal atau nominal?
Standar deviasi biasanya digunakan untuk data interval atau rasio, yang memiliki urutan dan jarak antara nilai-nilai yang dapat diukur. Untuk data kategorikal atau nominal, ukuran sebaran yang lebih cocok adalah proporsi atau persentase.
5. Bagaimana cara menafsirkan standar deviasi?
Tingkat standar deviasi mengindikasikan seberapa jauh data tersebar di sekitar nilai rata-ratanya. Semakin tinggi standar deviasi, semakin besar variabilitas dalam data. Sebaliknya, semakin rendah standar deviasi, semakin sedikit variasi dalam data.
Dengan memahami konsep standar deviasi, kita dapat menggunakan informasi ini untuk mengambil keputusan yang lebih baik dan memahami data dengan lebih baik dalam berbagai konteks. Standar deviasi adalah alat yang kuat untuk menganalisis sebaran data dan memiliki implikasi yang signifikan dalam berbagai bidang dan aspek kehidupan sehari-hari.